TIC-TAC: A Framework for Improved Covariance Estimation in Deep Heteroscedastic Regression

Megh Shukla, Mathieu Salzmann, Alexandre Alahi
International Conference on Machine Learning (ICML) 2024, Vienna

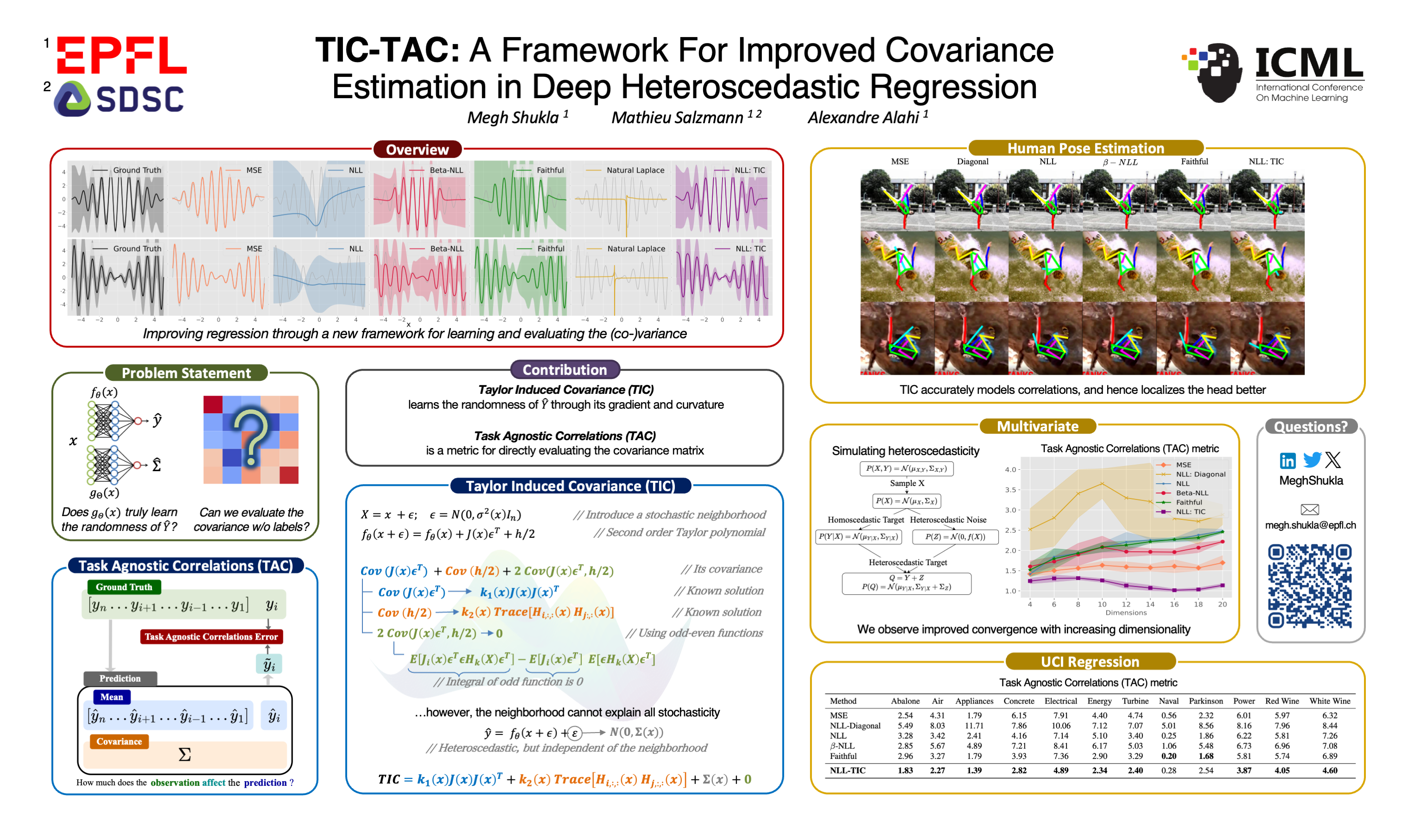
Problem Statement

When heteroscedastic models make predictions, they often estimate:

1. The mean value of the target.
2. The covariance which represents the uncertainty/variability of the target.

However, predicting this covariance is difficult because there are no ground-truth labels for this covariance. The standard approach without the ground-truth covariance relies on optimizing the negative log-likelihood to jointly learn the mean and covariance. However, recent works show that incorrect covariance estimates can lead to unstable training and ultimately affecting optimization.

Given samples from a noisy (shown as shaded region) sinusoidal, we compare different methods on their ability to learn the mean and variance.

While there have been multiple attempts to address this, we argue that many existing approaches use workarounds and may not truly solve the problem. For instance, recent works proposed different variations of the negative log-likelihood with varying degrees of effectiveness. Moreover, why should the predicted variance truly represent the randomness of the underlying target?

Therefore, we propose a solution that directly improves covariance estimation using a more mathematically grounded approach. With the Taylor Induced Covariance (TIC), we tie the predicted covariance to the gradient and curvature of the mean (target) estimator. Intuitively, The gradient and curvature quantify the variation in the prediction within a small neighborhood of the input. Large changes in the target for small changes in the neighborhood of the input should imply larger variance of the prediction.

Taylor Induced Covariance

With TIC, we propose a new method to parameterise the covariance. Specifically, TIC ties the randomness of the prediction to its gradient and curvature. We do this by representing the input using a stochastic neighbourhood, allowing us to take the second order Taylor polynomial. Specifically, if ε is our stochastic neighborhood, we get We solve for the covariance of this polynomial through simplifications and some help from our friend, the Matrix Cookbook. The detailed derivations is provided in Section 3. This gives us the final covariance: The presence of the jacobian and hessian allow us to define the covariance using the gradient and curvature of the prediction. We formalize this in the algorithm below.

Task Agnostic Correlations

While we have a new method for covariance estimation, how do we evaluate the covariance? Remember, we do not have labels for the covariance! With TAC, we propose a new metric to directly evaluate the covariance. Specifically, we reason that the goal of estimating the covariance is to encode the relation between the target variables. Therefore, partially observing a set of correlated targets should improve the prediction of the hidden targets since by definition the covariance encodes this correlation. TAC measures this improvement as an accuracy measure for the learnt correlations. We do this by conditioning the predicted target distribution over all but one ground truth, and observe the improvement in the target corresponding to the hidden target variable. If the correlations are learnt correctly, the prediction should update towards the hidden ground truth. By contrast, incorrect correlations move the prediction away from the ground truth. We formalize this through a schematic and algorithm

Moreover, TAC and the log-likelihood are complementary: while log-likelihood is a measure of optimisation, TAC is a measure of accuracy of the learnt correlations.

Experiments

We conduct experiments across real and synthetic datasets, spanning univariate and multivariate analysis. Our results show that TIC not only accurately learns the covariance, but also leads to improved convergence of the negative log-likelihood.

Univariate

We learn constant and varying amplitude sinusoidal with heteroscedastic noise. We observe that TIC accurately learns the variance and improves convergence of the negative log-likelihood. We also observe that modifications to the negative log-likelihood which are not valid distributions may result in unreliable variance estimates.

Multivariate

To evaluate the learnt covariance using ground truth, we setup an experiment with synthetic samples. The schematic is specified above, which allows us to draw samples from heteroscedastic distributions. We compare different methods simulating increasing dimensionality of the data. Our quantitative results show that the gap between TIC and other methods widens.

UCI Regression

We conduct experiments on datasets from the UCI Regression repository, and report significant performance gains on most datasets. A curious observation can be made with the Naval dataset, where TIC does not perform as well as other baselines. We note that TIC may not be suitable if all samples have a low degree of variance. A low degree of variance (as indicated by the likelihood) results in accurate mean fits, which implies that small gradients are being backpropagated, and in turn affecting the TIC parameterization. However, we argue that datasets with a small degree of variance may not benefit from heteroscedastic modelling.

2D Human Pose Estimation

We use two architectures: ViTPose and Stacked Hourglass for our studies in human pose estimation. We provide qualitative and quantitative results and show that TIC accurately learns the correlations underlying various human joints. Our qualitative results specifically show that TIC accurately localises the head given the location of other joints. This is especially true for complex poses. Our quantitative results show that TIC scales to both, convolutional and transformer based architectures and outperforms state-of-the-art in learning correlations across various human joints.

Conclusion

Our study is best concluded by the following points:
🔹 Old methods struggle with accurately predicting heteroscedasticity / uncertainty.
🔹 TIC improves this by mathematically modeling how predictions change.
🔹 TAC provides a better way to check if the uncertainty prediction is correct.
🔹 The result? More reliable models that learn faster and make better predictions!

Acknowledgement

We thank the reviewers, for their valuable comments and insights. We also thank Reyhaneh Hosseininejad for her help in preparing the paper.

This research is funded by the Swiss National Science Foun- dation (SNSF) through the project Narratives from the Long Tail: Transforming Access to Audiovisual Archives (Grant: CRSII5 198632). The project description is available on: https://www.futurecinema.live/project/

Citation

If our work is useful, please consider citing the accompanying paper and starring our code on GitHub!

@InProceedings{shukla2024tictac,
  title = {TIC-TAC: A Framework for Improved Covariance Estimation in Deep Heteroscedastic Regression},
  author = {Shukla, Megh and Salzmann, Mathieu and Alahi, Alexandre},
  booktitle = {Proceedings of the 41th International Conference on Machine Learning},
  year = {2024},
  series = {Proceedings of Machine Learning Research},
  month = {21--27 Jul},
  publisher = {PMLR}
}